Introduction
Historically, conventional high-order finite element methods were rarely used for industrial problems because the Jacobian rapidly loses sparsity as the order is increased, leading to unaffordable solve times and memory requirements [Brown10]. This effect typically limited the order of accuracy to at most quadratic, especially because quadratic finite element formulations are computationally advantageous in terms of floating point operations (FLOPS) per degree of freedom (DOF)—see Fig. 1—, despite the fast convergence and favorable stability properties offered by higher order discretizations. Nowadays, high-order numerical methods, such as the spectral element method (SEM)—a special case of nodal p-Finite Element Method (FEM) which can reuse the interpolation nodes for quadrature—are employed, especially with (nearly) affine elements, because linear constant coefficient problems can be very efficiently solved using the fast diagonalization method combined with a multilevel coarse solve. In Fig. 1 we analyze and compare the theoretical costs, of different configurations: assembling the sparse matrix representing the action of the operator (labeled as assembled), non assembling the matrix and storing only the metric terms needed as an operator setup-phase (labeled as tensor-qstore) and non assembling the matrix and computing the metric terms on the fly and storing a compact representation of the linearization at quadrature points (labeled as tensor). In the right panel, we show the cost in terms of FLOPS/DOF. This metric for computational efficiency made sense historically, when the performance was mostly limited by processors’ clockspeed. A more relevant performance plot for current state-of-the-art high-performance machines (for which the bottleneck of performance is mostly in the memory bandwith) is shown in the left panel of Fig. 1, where the memory bandwith is measured in terms of bytes/DOF. We can see that high-order methods, implemented properly with only partial assembly, require optimal amount of memory transfers (with respect to the polynomial order) and near-optimal FLOPs for operator evaluation. Thus, high-order methods in matrix-free representation not only possess favorable properties, such as higher accuracy and faster convergence to solution, but also manifest an efficiency gain compared to their corresponding assembled representations.
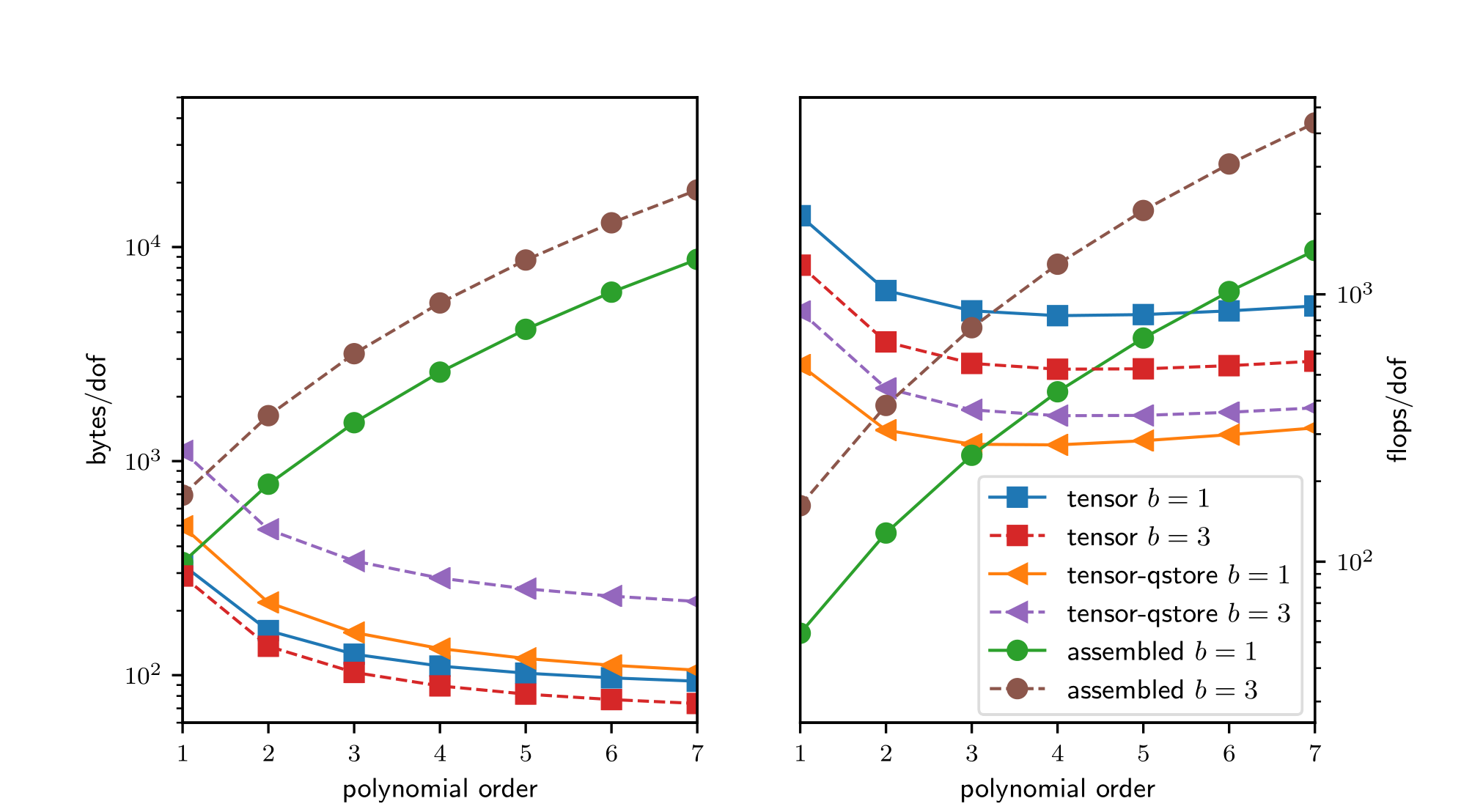
Fig. 1 Comparison of memory transfer and floating point operations per degree of freedom for different representations of a linear operator for a PDE in 3D with \(b\) components and variable coefficients arising due to Newton linearization of a material nonlinearity. The representation labeled as tensor computes metric terms on the fly and stores a compact representation of the linearization at quadrature points. The representation labeled as tensor-qstore pulls the metric terms into the stored representation. The assembled representation uses a (block) CSR format.
Furthermore, software packages that provide high-performance implementations have often been special-purpose and intrusive. libCEED [BAB+21] is a new library that offers a purely algebraic interface for matrix-free operator representation and supports run-time selection of implementations tuned for a variety of computational device types, including CPUs and GPUs. libCEED’s purely algebraic interface can unobtrusively be integrated in new and legacy software to provide performance portable interfaces. While libCEED’s focus is on high-order finite elements, the approach is algebraic and thus applicable to other discretizations in factored form. libCEED’s role, as a lightweight portable library that allows a wide variety of applications to share highly optimized discretization kernels, is illustrated in Fig. 2, where a non-exhaustive list of specialized implementations (backends) is provided. libCEED provides a low-level Application Programming Interface (API) for user codes so that applications with their own discretization infrastructure (e.g., those in PETSc, MFEM and Nek5000) can evaluate and use the core operations provided by libCEED. GPU implementations are available via pure CUDA and pure HIP as well as the OCCA and MAGMA libraries. CPU implementations are available via pure C and AVX intrinsics as well as the LIBXSMM library. libCEED provides a unified interface, so that users only need to write a single source code and can select the desired specialized implementation at run time. Moreover, each process or thread can instantiate an arbitrary number of backends.
Fig. 2 The role of libCEED as a lightweight, portable library which provides a low-level API for efficient, specialized implementations. libCEED allows different applications to share highly optimized discretization kernels.